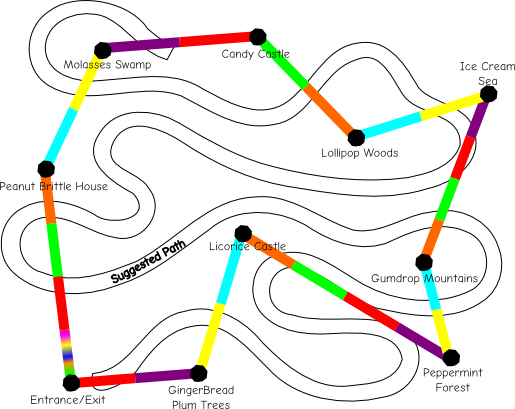
Candyland, a game where a group of children take a convoluted path through a diabetes filled paradise, needs a revision. No child should be exposed to such a gluttonous journey at such an early age. On the other hand, hipsterfying this into Vegatableland - where the Cookie Monster actively promotes carrots over cookies - is the legal definition of a dystopia. I believe a happy medium would involve a quick closed-loop tour of Candyland that does NOT end at King Candy's suspicious looking castle.
So, what is the best route that visits all the wonders of Candyland while minimizing the total distance traveled. Well, this is just the famous traveling salesman problem! Using a simulated annealing approach my proposed path is:
from math import sqrt, exp
import random
import copy
import matplotlib.pyplot as plt
locations = {
'entrance': (198, 265),
'gingerbread': (324, 271),
'peppermint': (572, 287),
'gumdrop': (546, 385),
'licorice': (368, 410),
'peanut': (170, 476),
'lollipip': (480, 508),
'icecream': (613, 553),
'molasses': (226, 594),
'candycastle': (382, 609)
}
def distance(loc1, loc2):
'''
Finds the Euclidean distance between two locations
'''
x1, y1 = locations[loc1]
x2, y2 = locations[loc2]
return sqrt((x1 - x2) ** 2 + (y1 - y2) ** 2)
def cost(route):
'''
Calculates the total distance of a route
'''
total_distance = 0
for index, city in enumerate(route):
total_distance += distance(city, route[index - 1])
return total_distance
def neighbor(route):
'''
Alters the route by swapping two locations
'''
index1 = random.randint(1, len(route[:-2]))
index2 = random.randint(1, len(route[:-2]))
route[index1], route[index2] = route[index2], route[index1]
return route
def boltzmann_prob(old_cost, new_cost, T):
'''
Compares both routes via the Boltzmann factor at a
given 'temperature' (T)
'''
try:
return exp(-(new_cost - old_cost) / T)
except OverflowError:
return 1
def anneal(route):
'''
Finds the best route by swapping locations continuously while the
probabiliy to switch routes gradually decreases
'''
old_cost = cost(route)
T = 1E4
T_min = 1E-3
decay = 0.95
while T > T_min:
for i in range(1000):
new_route = neighbor(route)
new_cost = cost(new_route)
prob = boltzmann_prob(old_cost, new_cost, T)
if prob > random.random():
route = new_route
old_cost = new_cost
ideal_route = copy.copy(route)
T = T * decay
return ideal_route
def plot_tour(tour):
X, Y = zip(*[locations[point] for point in tour])
plt.plot(X, Y, 'b')
plt.axis('scaled')
if __name__ == "__main__":
route = locations.keys()
route = route + [route[0]]
best_route = anneal(route)
plot_tour(best_route)
plt.show()