As I write this, I'm taking a break from searching for my recently wandered off and phoneless wife. I wish to find her as quickly as possible, but I'm currently experiencing some inner turmoil. Should I continue on this wife-hunt or is it more time-efficient to remain stationary and wait until she walks by? Do two confined random-walks meet quicker than a single random-walk finding a stationary point? Wait a second, I can write a script that simulates finding my lost and (presumingly) scared wife!
import random
import numpy as np
ARRAY_SIZE = 10
NUM_TRAILS = 10000
def initial_location():
'''
Creates a random starting point on a ARRAY_SIZE by ARRAY_SIZE grid
'''
return [random.randint(0, ARRAY_SIZE), random.randint(0, ARRAY_SIZE)]
def get_possible_directions(location):
'''
This ensures the person stays within the grid, the bottom left is [0,0]
'''
possible_vertical = [0]
possible_horizontal = [0]
# if you're not on the right border, you can go East
if location[0] < ARRAY_SIZE:
possible_horizontal.append(1)
# if you're not on the left border, you can go West
if location[0] > 0:
possible_horizontal.append(-1)
# if you're not on the top border, you can go North
if location[1] < ARRAY_SIZE:
possible_vertical.append(1)
# if you're not on the bottom border, you can go South
if location[1] > 0:
possible_vertical.append(-1)
return map(random.choice, [possible_horizontal, possible_vertical])
def update_location(initial_location):
'''
Selects a random direction and move there
'''
selected_location = get_possible_directions(initial_location)
new_location = np.add(initial_location, selected_location)
return new_location
def simulate_partner_finding():
chris_location = initial_location()
chelsea_location = initial_location()
counter = 0
while not np.array_equal(chris_location, chelsea_location):
chris_location = update_location(chris_location)
# Comment out 'chelsea_location' to keep her stationary
chelsea_location = update_location(chelsea_location)
counter += 1
return counter
def main():
counter_results = []
for trials in xrange(0, NUM_TRAILS):
counter_results.append(simulate_partner_finding())
print 'Average Number of Spaces: {0}'.format(np.mean(counter_results))
if __name__ == "__main__":
main()
In order to keep things simple, I'll assume this mall is a bounded square grid where my wife and I are initially assigned to a random location. Then, during each iteration, a non-stationary person walks a single square in any horizontal, vertical or diagonal direction. Whenever my wife and I are in the same square, I will record the total number of squares traveled and reset the simulation. This process repeats for two scenarios: 1) We're both randomly moving around 2) One person remains stationary, until representative total-distance averages are reached.
The diagram below shows a typical example for each scenario:
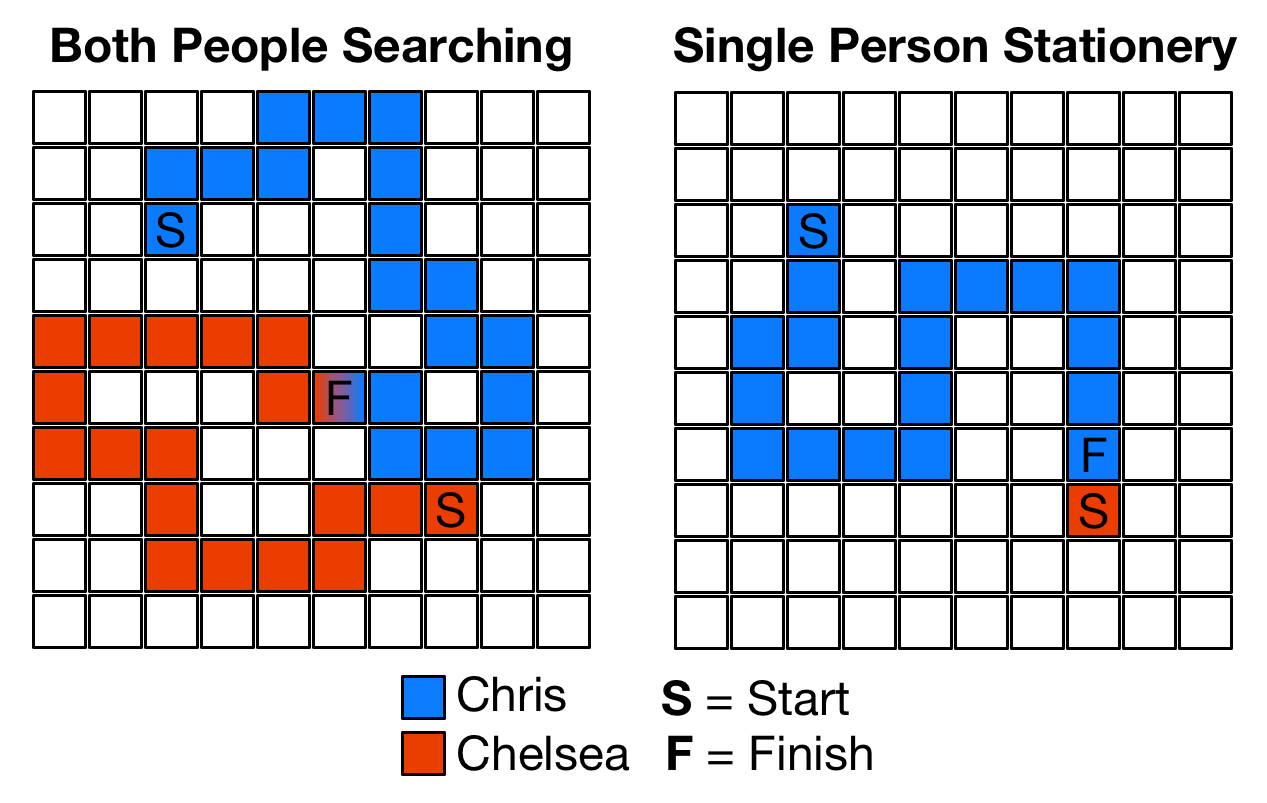
After running this simulation for a few different sized grids, I confirmed that two people randomly walking around is approximately 1.5x faster! Now, I would typically follow this result, but my wife already found me like 45 minutes ago and she's been patiently waiting for me to finish this blog post.